Bernoulli's Theorem In Hindi | बरनौली प्रमेय लिखिए |बरनौली प्रमेय की उत्पत्ति

बरनौली प्रमेय Bernoulli's theorem

Bernoulli's Theorem In Hindi (बरनौली प्रमेय लिखिए)

बरनौली प्रमेय प्रमेय तरल की गति में उर्जा संरक्षण के सिद्धान्त पर आधारित है। इस नियम के अनुसार,

जब कोई अश्यान व असम्पीड्य तरल एक स्थान से दूसरे स्थान तक धारा रेखीय प्रवाह में प्रवाहित होता है तो मार्ग के प्रत्येक बिन्दु पर इसके एकांक आयतन की कुल उर्जा अर्थात् दाब उर्जा, गतिज उर्जा तथा स्थितिज उर्जा का योग नियत रहता है।

अर्थात् प्रति एकांक आयतन द्रव प्रवाह के लिये

उपरोक्त समी. में ρg से भाग देने पर

 h + v²/2g +  P/ρg  = नियतांक

                       

इस समीकरण में h को गुरूत्वीय शीर्ष, v²/2g को वेग शीर्ष तथा P/ρg को दाब शीर्ष कहते है। इन तीनों के योग को सम्पूर्ण शीर्ष कहा जाता है।

अतः बरनौली की प्रमेय को निम्न प्रकार से भी कहा जा सकता है :- धारा रेखीय प्रवाह में किसी आदर्श द्रव (अश्यान व असम्पीड्य ) के किसी बिन्दु पर गुरूत्वीय शीर्ष, दाब शीर्ष तथा वेग शीर्ष का योग नियत रहता है।

जब प्रवाह क्षैतिज तल में हो h₁ = h₂

P1 +1/2ρv₁²+ρgh1 = P2+1/2ρv2²+ρgh2

P1 +1/2ρv₁² = P2+1/2ρv2²

बरनौली प्रमेय के समीकरण से यह स्पष्ट है कि किसी बहते हुए द्रव के जिस स्थान पर द्रव का वेग कम होता है, वहां दाब अधिक होता है तथा जिस स्थान पर वेग अधिक होता है वहां दाब कम होता है।

बरनौली प्रमेय की उत्पत्ति

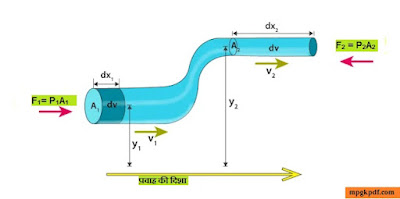
माना कोई असम्पीड्य तथा अश्यान द्रव किसी असमान अनुप्रस्थ काट वाली नली में धारा रेखीय प्रवाह  में प्रवाहित हो रहा है जैसे चित्र में दिखाया गया है।

माना अनुप्रस्थ काट X का क्षेत्रफल A1 तथा दाब P1 है एवं इसकी पृथ्वी से ऊंचाई h1 है। तथा अनुप्रस्थ काट Y का क्षेत्रफल A2 तथा दाब P2 है एवं इसकी पृथ्वी से ऊंचाई h2 है। 

चूंकि Y का क्षेत्रफल (A2) X के क्षेत्रफल (A1) से कम है। अतः अविरतता के सिद्धांत से Y का वेग V2, X के वेग V1 से अधिक होगा।

माना द्रव का प्रवाह X सिरे से 1 सेकेंड के लिए होता है जिसमें वह V1 दूरी तय कर लेता है इस पर (P1 × A1) का बल आरोपित होता है तो एक सेकेंड में X सिरे में प्रवेश करने वाले द्रव पर किया गया कार्य

W1 = P1 x A1 x V1

इसी प्रकार Y सिरे पर कार्य

W2 = P2 x A2 x V2

अत: द्रव पर किया गया कुल कार्य

W = W1-W2

W = (P1 x A1 x V1) - (P2 x A2 x V2)

चूंकि सततता के समीकरण से प्रत्येक काट पर एक सेकंड में प्रवाहित आयतन समान होता है तो

A1 V1 =  A2 V2 = V आयतन

तो कार्य 

W = (P1-P2)V

W = (P1-P2)m/ρ   …………….(1)

यदि 1 सैकंड में X सिरे पर प्रवेश करने वाले द्रव की गतिज ऊर्जा 1/2mv12 तथा Y सिरे पर 1/2mv22 है 

तो गतिज ऊर्जा में परिवर्तन

∇K = 1/2mv2² - 1/2mv₁²

∇K = 1/2m(v2²-v₁²) ……………..(2)

अब X सिरे की स्थितिज ऊर्जा mgh1 तथा Y सिरे पर स्थितिज ऊर्जा mgh2 है तो

स्थितिज ऊर्जा में परिवर्तन

∇U= mgh2 -mgh1

∇U= mg(h2 -h1) ……………….(3)

चूंकि द्रव की ऊर्जा में परिवर्तन उसमें किए गए कार्य के कारण ही होती है तो

W=∇K+ ∇U

समी.1,2 व 3 के मान रखने पर

(P1 – P2)m/ρ = 1/2m(v2²-v₁²)+mg(h2 -h1)

P1 – P2 = 1/2ρ (v2²-v₁²)+ρg(h2 -h1)

P1 +1/2ρv₁²+ρgh1 = P2+1/2ρv2²+ρgh2

अत:

Also Read....

बरनौली प्रमेय लिखिए

धारा रेखीय एवं विक्षुब्ध प्रवाह

ऊष्मागतिकी क्या है, ऊष्मागतिक निकाय, ऊष्मागतिक साम्य स्थित

ऊष्मागतिकी का प्रथम नियम

ऊष्मागतिकी का द्वितीय नियम ऊष्मागतिकी का प्रथम नियम की कमियाँ

ऊष्मा इंजन तथा दक्षता, ऊष्मा इंजन के प्रमुख भाग

ऊष्मागतिक फलन या ऊष्मागतिक विभव 

तापीय साम्य तथा ऊष्मागतिकी का शून्यवाँ नियम